Compounding – Unfortunately, this is one concept which most people would have studied in school days, but no longer seem to remember.Caution: If you don’t understand this concept now, you can loose a lot of money in future. As a reminder, compounding refers to the re-investment of income at the same rate of return to constantly grow the principal amount, year after year. Suppose you put Rs 1,00,000 in a bank fixed deposit giving 8% annual returns (lets ignore taxes for simplicity).
Now after a year, your principal of Rs 1,00,000 would have earned Rs 8000 in interest. If you reinvest that interest(Rs 8000) along with the original Rs 1,00,000, what will happen in next year? You will get another Rs 8000 from your original Rs 1,00,000 investment, plus Rs 640 from the reinvested Rs 8000.
If you reinvest all your returns, the total value of your original Rs 1,00,000 investment after 5 years would be as follows:
At end of Year 1: Rs 1,00,000 earns 8% = Rs 1,08,000
At end of Year 2: Rs 1,08,000 earns 8% = Rs 1,16,640
At end of Year 3: Rs 1,16,640 earns 8% = Rs 1,25,970
At end of Year 4: Rs 1,25,970 earns 8% = Rs 1,36,050
At end of Year 5: Rs 1,36,050 earns 8% = Rs 1,46,930
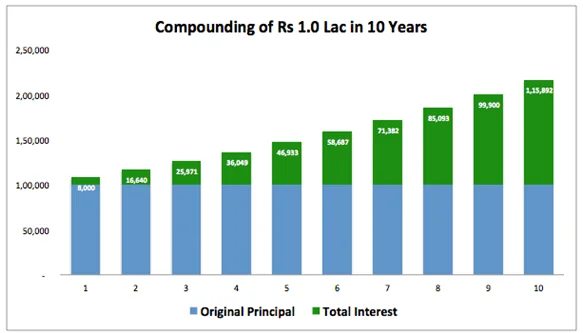
And when we allow this compounding to continue for 10 years, the result is this:
Now this was about fixed deposits. But what about stock markets?
Historically, stocks have given average returns of close to 12% every year. Now if we use 12% in our calculation of Rs 1 lakh original investment, we get the following numbers:
At end of Year 1: Rs 1,00,000 earns 12% = Rs 1,12,000
At end of Year 2: Rs 1,12,000 earns 12% = Rs 1,25,440
At end of Year 3: Rs 1,25,440 earns 12% = Rs 1,40,493
At end of Year 4: Rs 1,40,493 earns 12% = Rs 1,57,352
At end of Year 4: Rs 1,40,493 earns 12% = Rs 1,57,352
You might feel that this is not as great as we are trying to make it sound. After all, you only get about Rs 76,000 extra after 5 years.
Think about it.
But here comes the main part. Time is the key to allow compounding to show its magic. Over short periods, compounding produces a little extra return (as seen above). But over long periods, it can have enormous impact on final returns.
To illustrate this, suppose the above process continues till the 15th year. Do you have any idea what the amount will become?
At end of Year 15: Rs 5.5 lakhs
And what if it goes on even beyond 25th year?
At end of Year 25: 17.0 lakhs
At end of Year 26: 19.1 lakhs
At end of Year 27: 21.3 lakhs
At end of Year 28: 23.9 lakhs
At end of Year 29: 26.7 lakhs
At end of Year 30: 29.9 lakhs
Now do you see what compounding does to your money? And do you remember that the only investment that was made was Rs 1 lakh at start. Not even one more rupee was invested after that.
Have a look at the graph below:
This is the real power of compounding. Now just imagine what would have been your returns if you had additionally, invested more money every year.
It would be in crores of Rupees.
For compounding to work, two things are required. First is of course, the re-investment of earnings. And second is, long periods of time. The more time you give your investments, the more you would be able to accelerate the process of compounding of your original investment.
So if you are a long term investor, you need to understand that you don’t need to find multibaggers every now and then. Of course it helps if you do. But it’s not as easy as it sounds. A more practical and doable approach is to start investing early and allow your investments the time, to grow and compound.
It is speculated that Albert Einstein called compounding as “the greatest mathematical discovery of all time”. Once you understand this beautiful concept, you will know exactly what he meant.



